最近在师兄的推荐下,阅读了一篇利用半监督图做PolSAR图像分类的文章,感觉这篇文章整体思路不错,值得借鉴。在这里做一下简单的笔记。
基本信息
- 年份:2019
- 期刊:IEEE Transactions on Geoscience and Remote Sensing
- 标签:Graph, PolSAR, Semisupervised
- 数据:Flevoland、San Francisco
创新点
- 第一个将半监督图分类算法和深度卷积神经网络融合于PolSAR图像分类框架中 。
- 设计了结合半监督项、CNN项、成对平滑损失项的能量函数。其中:
- 半监督项强迫类标预测受人类标记样本的约束
- CNN项负责提取具有分辨性的PolSAR特征并预测类标
- 成对平滑损失项负责预测类标和图像边缘对齐
- 设计了一个迭代、交替的优化过程优化模型
创新点来源
监督方法类似于现有的深度学习方法能够实现很高的分类正确率,但是严重依赖于大量的标记样本。无监督方法简单并且效率高,但是大部分正确率不高。半监督方法结合了监督和半监督方法的优点,比较适合基于少量标记样本做分类问题。
基于半监督图的方法因为扎实的数学基础以及对像素内在结构的出色表征,是一个典型的半监督学习方法。但是基于半监督图的方法有两个任务:
- 如何得到更有表现力的极化特征
- 如何基于图做类标传播
针对这两个问题,论文做了如下工作:
- 为了得到更有表现力的极化特征,引入深度学习方法
- 为了更好的基于图做类标传播,在能量函数中引入了半监督项、成对平滑损失项
- 为了在一个框架中兼顾上面两个问题,提出交替迭代能量函数的方法
主要过程
符号
PolSAR特征使用$X \in R^{D_1 \times D_2 \times D_3}$表示,其中$D_1$和$D_2$分别表示高和宽,$D_3$表示特征的维度,总的像素个数为$N=D_1 \times D_2$。已知标记样本用$L=\{(x_1,t_1);(x_2,t_2);…;(x_n,t_n)\}$表示,其中$n \ll N$,$t_i \in \{ 1,2,..,K\}$,$x_i \in S_{sup}$,$K$是类别总数,$S_{sup}$是标记样本集合。所有样本的标记用$Y=\{ y_i\},i \in \{1,2,…,N \}$表示。
整体框架
下图展示了所提方法的框架,它将半监督图和深度神经网络统一到了一个框架中。给定PolSAR图像,建立图结构,这可以看做是Markov random field(MRF)。监督项使得类标预测受到随机选取的人工标记样本影响,CNN向MRF输出像素预测。成对平滑损失项使得标签在传播过程中更加平滑。
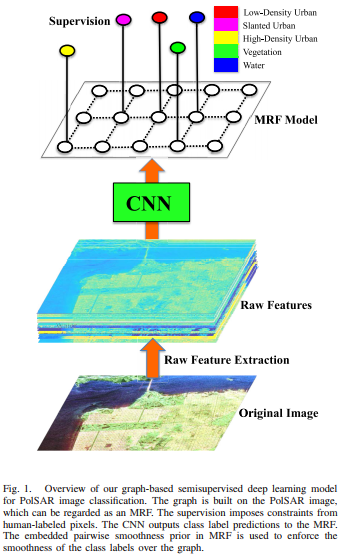
初始特征提取
一般PolSAR数据使用的相干矩阵表示,它是复数形式的,而神经网络的输入一般是实数形式的,所以论文中采用如下方式得到PolSAR的初始特征表示:
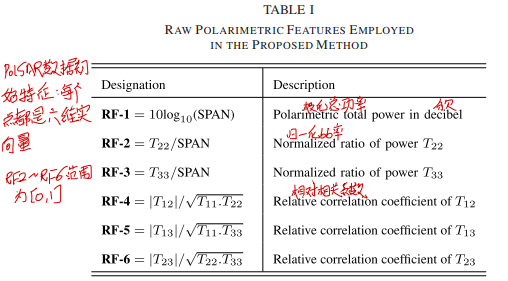
这种表示形式和论文《Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks》中的表述形式一致。
能量函数
能量函数分为三部分,整体结构如下所示。要利用能量函数优化两个参数——所有像素的预测结果$Y$、CNN参数$F_\theta$。
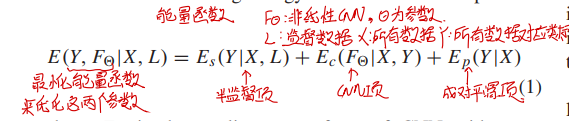
半监督项
半监督项约束有标记像素的类别不变性 ,基于随机选择的人工标记样本$L$,定义为:
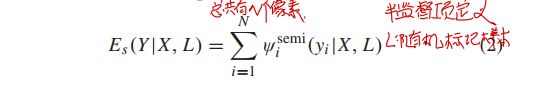
其中,$\Psi_i^{semi}(y_i|X,L)$的定义如下:
不过这项有一个问题,对于未标记样本在这一项中其实是常数在优化过程中并不起到任何作用。而若去掉该项中的未标记样本,则这项可以称作是监督项。
CNN项
上面已经知道了CNN输入初始特征,另外还需要注意的一点是,CNN的输入是三维向量,所以实际在使用的时候,需要结合输入一个个的PolSAR特征块(论文中为8x8x6)。即输入到CNN的每个样本均是8x8的区域,而不是单个像素点。
CNN各层之间的运算这里就不再赘述了,只说下能量损失的CNN项,其定义其实就是一般的交叉熵损失函数。
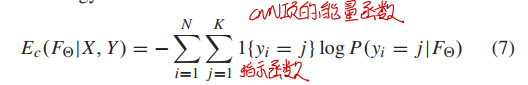
成对平滑项
成对平滑项强迫邻域像素有相似的类标。具体定义如下:

关于这一项除了我在图上的标注之外,这样理解更加合理一点:当$v_i$和$v_j$比较接近时,等号右边的指数项比较大,为了使右边整体比较小,需要$y_i$和$y_j$尽可能的接近,进而实现成对平滑损失约束。当$v_i$和$v_j$相差较大时,等号右边的指数项比较小,整体损失就比较小,对$y_i$和$y_j$之间相关性的约束也就比较小。
把这三项具体再下来如下所示:

能量函数分为三部分,可以让预测的类标结果受到人工标记信息、CNN预测结果、类标平滑(空间信息)的影响。最小化能量函数的作用是让预测类标更加平滑,且和人工标记结果、CNN预测结果一致。
优化过程
由能量函数可以看出,需要优化两个参数所有像素的预测结果$Y$、CNN参数$F_\theta$。所以可以将整个优化分为两个子问题——CNN学习子问题和标签传播子问题。
CNN学习子问题
当样本类别$Y$固定时,优化CNN$F_\theta$中的参数$\theta$。此时由于$Y$固定,半监督项和成对平滑项不计入能量函数,所以只对能量函数中的CNN项优化。
CNN优化第一步:先借助K-Wishart或者超像素分割方法得到PolSAR图像所有像素类标$Y$,并作为监督信息。初始化CNN中的全部网络参数$\theta$,对所有像素预测一个结果$\hat Y$。由$Y$和$\hat Y$计算能量函数中的CNN项,由反向传播算法对CNN网络参数$\theta$优化。最后利用优化过的CNN网络对PolSAR所有像素进行新的预测$Y$。
CNN优化除了第一步:与CNN优化第一步不同的是,这里的监督信息——PolSAR像素图像像素类标$Y$取得是上一步标签传播的结果。
标签传播子问题
当CNN$F_\theta$中的参数$\theta$固定,优化算法基于监督信息、CNN预测和类标光滑约束将类标传播至未标记像素,以此优化样本类别$Y$。此时由于$\theta$固定,CNN项不计入能量函数,所以只对能量函数中的半监督项和成对平滑项优化。
这个优化问题是一个组合优化问题,可以视为标准的MRF模型。图上的类标$Y$组成了MRF模型,半监督项和成对平滑项组成上面的能量函数。
MRF优化是NP难问题,但是可以使用graph cut或者belief propagation算法优化。后者使用的是“up-down-left-right”消息传播策略,使得收敛速度更快。所以论文中使用的是belief propagation算法
初始化过程
前面说过CNN第一步优化需要PolSAR图像的全部类标信息$Y$作为监督信息,但是因为只知道极少标记的样本。所以就需要借助这些极少标记的样本对PolSAR图像整体的类别信息做初步预估。
优化过程主要有两种方法——K-Wishart初始化方法和超像素初始化方法。
K-Wishart初始化
基于K-Wishart距离,提出半监督K-Wishart初始化方法。
不同于无监督K-Wishart分类方法,我们把已经给出的标记像素作为监督信息,给出初始聚类中心(例如取每一类的所有标记样本的平均值),然后使用K-Wishart聚类算法迭代优化聚类中心和类标标记。
超像素初始化
因为PolSAR图像是空间连续的,所以邻居像素应该具有相同的类标。基于这个启发性先验,PolSAR图像应该可以被分割成不同的小同质区域,即superpixels where pixels inside share the same class labels. 所以,如果一个超像素中有一个标记样本,那么该超像素中其他区域应该被初始化为相同的类标。因为可用的标记样本特别少,所以利用这种方式是一种很好的初始化途径。
在本论文中,我们使用了SLIC方法作用于PolSAR的PauliRGB图上,得到超像素分割图。然后根据超像素分割结果,将给定的标记信息传播到同质未标记样本上。
算法过程
值得注意的是,在整个算法之前,论文使用了Lee滤波器对斑点噪声进行了抑制。

思考
这篇论文信息量还是挺大的,有好几个地方暂时还没有搞清楚,不过可以得到好几个启发:
(1)之前个人觉得半监督方法的主要途径是如何很好的将可靠的未标记样本添加到已知标记样本中,然后对模型优化。在这个过程中,不可靠样本并没有参与到模型的优化。而本论文中提到了另外一种半监督思路:全部样本均参与模型的优化,在模型的优化过程中要做到:
利用有限的标记样本,很好地对所有数据的标签进行初始化(论文中体现为两种初始化方法)
不断优化未标记样本的可靠性(论文中体现为CNN项和成对损失项)
- 保留已标记样本的可靠性(论文中体现为半监督项)
而为了在模型优化时同时做到这几点,论文中提到了交叉迭代优化的方法。
(2)PolSAR分类时,要利用空间信息。例如本文中的超像素初始化以及成对平滑损失。
缺点
(1)算法整体并没有端到端训练,整体方案复杂
(2)优化过程不仅涉及到CNN的优化,还涉及到对MRF模型的优化
(3)能量函数的半监督项中未标记样本并不起到任何作用,可以退化为监督项
疑惑
论文题目是基于半监督图的,可是个人觉得只有在成对平滑项中能够体现出相似性度量(图边的权重),其余地方并没有体现图。
答:这里的半监督图确实体现在成对平滑项中,在该项中定义了相似性,可以得到图结构。本文只是借助图结构定义了成对平滑项(图正则项),进而实现标签传播(这个图正则项优化时使用了MRF,其实还有别的优化思路,MRF不是本文的重点)。而GNN也有类似的图结构,不过需要借助图上的卷积运算实现标签传播。

